Logarithms are used many scientific calculations. Many scientific laws must be expressed in either exponential or logarithmic form. As a consequence, calculations involving these laws must also used exponents and logarithms. There are two types of logarithms, common logarithm (base 10) and natural logarithm (base e). Chemists uses logarithms extensively. Here are some examples.
In chemical kinetics, rate constants for most reactions closely follow an equation, called Arrhenius rate law or Arrhenius equation:
k = A e -Ea/RT
e is the base of natural logarithms, 2.718...
Ea is the activation energy
R is the gas constant, 8.31 J/K mol
This equation represents the relationship of rate constant k and temperature T.
Often it is useful to recast Arrhenius equation in logarithm form. Taking the natural logarithm of both sides of the equation gives
ln k = lnA - Ea/RT
or, expressed in terms of base-10 logarithm,
Log k = logA - Ea/2.303RT
The reason for using logarithm form is that if we plot log k against 1/T, we should get a straight line. The slope of this line is -Ea/2.303R. This is how we obtain the activation energy.
Another example of using logarithm in chemistry is acidity pH and basicity pOH, where pH = - log [H+] and pOH = -log [OH-]. The reason for using this form is that in most case, the concentrations of H+ or OH- ions are very small number. Logarithm expression makes these values easy to use.
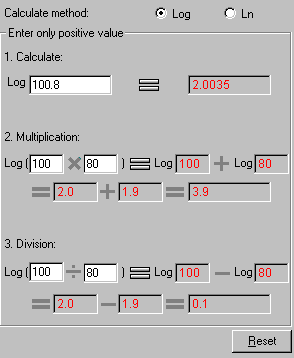
This module allows calculation of logarithms, including multiplication and division, with both the common and natural logarithms.
Special Input Instruction: To enter an exponent, use e-form, for example, to type in 1.1x102, enter 1.1e2.
This calculates the operation of logarithm of any given number. This functions the same as typical scientific calculator. Positive numbers only.
Select Log or Ln. Enter the number on the left box and click = to display the result.
The multiplication of two numbers inside logarithm equal to the sum of the logarithms of each number, with any base.
Log(AxB) = LogA + LogB
Ln(AxB) = LnA + LnB
Enter two numbers in the boxes on the left and click = to display the result.
The division of two numbers inside logarithm equal to the difference of the logarithms of these numbers, with any base.
Log(A/B) = LogA - LogB
Ln(A/B) = LnA - LnB
Enter two numbers in the boxes on the left and click = to display the result.